《统计学习方法》

九月 3, 2021 Book 本文总阅读量次

【书籍阅读】《统计学习方法》

一. 统计学习方法概论：

首先，要明确计算机科学中存在三个维度：系统，计算，与信息。统计学习方法（机器学习）主要属于信息这一维度，并在其中扮演者核心角色。

1. 监督学习概念：

监督学习，Supervised learning，指在已经做好标注的训练集上学习，为了叙述方便，定义以下基本概念：

输入空间（X），输出空间（Y）：输入所有可能取值，输出所有可能取值；

特征空间：输入一般由特征向量表示，所有特征向量存在的空间称为特征空间，输入空间与特征空间并不完全等价，有时需要映射；

上标 x^i^ :表示一个输入的第 i 个特征；

下标 x~j~：表示第 j 个输入。

回归问题：输入输出都为连续型变量；

分类问题：输出变量为有限个离散型变量；

标注问题：输入与输出变量都为变量序列。

假设空间：所有可能的模型的集合，也就是学习的范围。

使用训练集学习——>对未知数据进行预测

2. 统计学习三要素：

统计学习三要素为：模型，策略，算法；

模型是决定学习的预测函数的类型；

策略是判定什么样的模型是好的，用于度量当前的模型好坏；

算法是训练过程中的具体做法，例如如何回归，如何计算，如何调整等。

3. 模型的衡量方法：

损失函数与风险函数：

损失函数，Loss Function，用于模型一次预测的错误程度，例如：

损失函数的数值越小，模型就越好。如果计算损失函数的期望，得到的就是风险函数，Risk Function:

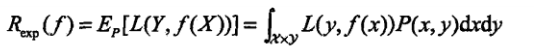
可以看出，损失函数用于某次预测的估计，风险函数用于总体平均估计。我们当然希望训练出的模型的风险函数越小越好。

但是，观察上式，理想化的概率分布P(x，y)是未知的，我们进行学习就是要通过模型来模拟它，故这个式子理论存在，实际不能计算，不能用作评估模型的直接方法。

经验风险与结构风险：

为了解决上述问题，我们引入经验风险：

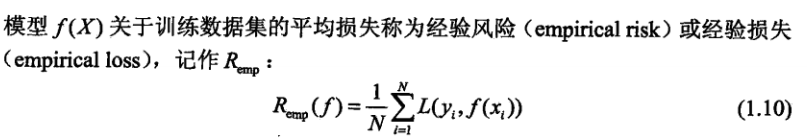
可以看到，经验风险将每个样本视作等概率出现，是模型对于训练集的平均损失，那么其与风险函数的误差在哪？

根据大数定律，当训练集足够大时，二者是近似相等的。但实际情况下，很多时候训练样本数目有限，甚至很小，故用经验风险效估计风险函数并不理想，故需要进行修正，这就是监督学习中的两个基本策略：经验风险最小化和结构风险最小化。

如果训练样本容量较大，使用经验风险最小化没什么问题。

当样本容量很小时，仅仅使用经验风险最小化容易导致过拟合，故这里使用结构风险（就是正则化）最小化方法，对模型复杂度进行惩罚，后续介绍。

训练误差与测试误差：

训练误差本质上不重要，它可以反应一个问题是不是容易学习，但要衡量模型的预测能力，主要是看测试误差。

正则化与交叉验证：

正则化是在经验风险项后再增加一个正则化项（Regularizer），其与模型的复杂度成正相关，一般使用模型参数向量的范数：

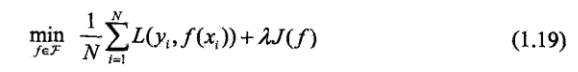
交叉验证的基本思想是重复使用数据：
1. 简单交叉验证：
  
  将训练集随机分为两部分，一部分训练，一部分测试，然后在各种条件下训练出不同的模型，用测试集进行横向对比，选出最好的。
  1. S折交叉验证：
  S-fold cross validation，随机地将已给数据切分为S个互不相交的大小相同的子集，选取S-1个用于训练，剩下一个用于测试。
  
  这样总共测试集有S种选法，将这S种全部试一遍，评选S次测评中平均误差最小的模型。
  1. 留一交叉验证：
  令S=N（训练集大小）即可，这种方法往往是在数据集特别缺乏的情况下使用。
泛化误差与泛化上界：

泛化能力指模型对位置数据的预测能力，就是模型的好坏。如何量化这个能力？

根据定义，其就是模型在测试集上的测试表现：

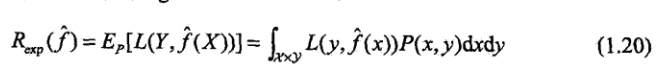
同时可以用以下式子衡量泛化误差的上界：
生成模型与判别模型：

监督学习方法又可以分为两种方法：生成方法（Generatice Approach）和判别方法（Discriminative Approach）。

如果以概率论的角度来看待，模型的作用是根据P（x）来求P（y | x），故下面有两种方法求

P（y | x），直接模拟P（y | x）和通过求 $P(\frac{y}{x}) = \frac{P(x,y)}{P(x)}$ 来求P（y | x）。

前者就是判别模型，后者是生成模型。

生成模型可以还原出联合概率分布P（x , y），学习收敛速度更快，可以适应存在隐含变量的情况；

判别模型直接学习条件概率,直接面对预测，准确率更高，并且简化了学习问题。

二. 感知机

感知机，perceptron，是二分类的线性分类模型，输入为特征向量，输出为类别，取1和-1两种。

感知机属于判别模型。

对于一个给定数据集，T = {（x~1~，y~1~）……（x~n~，y~n~）}，如果存在某个超平面S，w·x + b = 0（这里w是超平面的法向量，b是截距），使得所有 y~i~ = 1 的实例i，有 w·x~i~ + b > 0，y~i~ = -1则相反，则称数据集T为线性可分数据集（Linealy separable data set），否则，称数据集T为线性不可分数据集。

2.1 感知机损失函数：

感知机的目的就是对于一个线性可分的数据集，通过找出w和b，来确定一个超平面用于分类。

这里，我们选取某错误分类点到超平面S的总距离来当做损失函数，某一点到超平面S的距离如下：

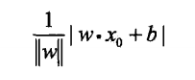
‖w‖是w的L~2~范数。

故，某个误分类点到超平面S的距离是：

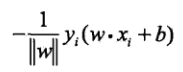
将所有误分类点求和，忽略L~2~范数，即可得到感知机的损失函数（M为误分类点集合）：

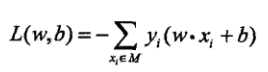
对于一个特定样本点的损失函数，在误分类时是参数w,b的线性函数，在正确分类时是0，故给定训练数据集T，损失函数L是w，b的连续可导函数。

2.2 训练过程：

感知机训练采用随机梯度下降的方法：

当找到一个误分类点时，不断梯度下降直至该点被正确分类为止。

数学证明其收敛性：

具体见书本，这里略过。

2.3 感知机的对偶形式：

由图可以看到，对于每个测试集中的x~i~，都有一个与之对应的α~i~，对偶形式中就是调整其对应的α。

关于gram矩阵的作用，如果手算一遍简单的训练过程，就可以得到答案。

三. k近邻法

k近邻法是一种基本的分类与回归方法，这里只讨论分类方法。

其输入为特征向量，输出为实例的类别，可以取多类。

3.1 算法描述：

给定一个训练集，对于新的数据实例，在训练数据集中找到与其最邻近的k个实例，这k个实例多数属于某个类，就把该输入实例分为这个类。

k近邻法没有显式的学习过程。可以理解为，k近邻算法将特征空间划分为了一些子空间，每个点所属的空间是确定的。

如何度量两个特征之间的距离？

k邻近模型的特征空间一般是n维实空间R^n^，使用欧氏距离或者L~p~距离（L~p~ distance），Minkowski距离（Minkowski distance）；

L~p~距离：

欧氏距离：

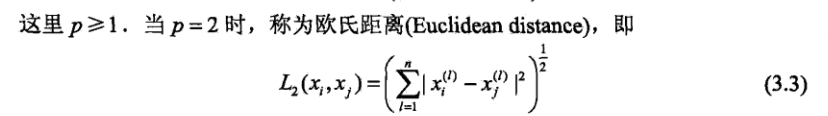
曼哈顿距离：

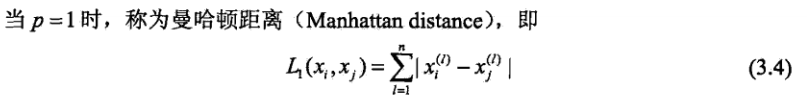
无穷距离：

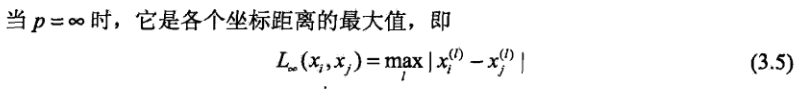
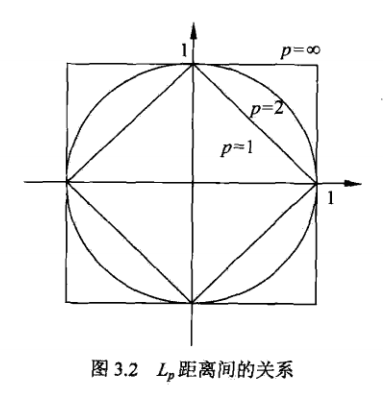
由下图可以看出，p取值不同时到原点距离为1的图形是不同的：

如何选择k的值？

k值越小，模型学习时的近似误差越小，估计误差越大，模型会越复杂，抗干扰性越小（例如，最邻近的点是噪声），模型会非常敏感，容易过拟合；

k值越大，估计误差会很小，近似误差会很大，整体模型变得简单。

k一般的取值并不大，使用交叉验证的方法来选取最佳的k值。
如何决策？

在得到k个最相似的实例后，采用何种规则判断测试样本属于哪一类呢？

k邻近算法使用多数表决的方法：

ps: ci表示某种决策规则下一组测试用例的表决结果。经由以上推导可以得出，多数表决规则是合理的。

如何快速找到某个用例的K近邻点？

KD树： 具体算法见书。