LLM ranking/reranking
Ranking/reranking methods with LLMs.
LLM Learning-To-Rank (LTR)
Under recommendation scenariom, the concept of learning-to-rank (LTR) means given the query $Q$, and passages $P$, output the top k most related passages with the query by using LLM. Funciton $R(Q, P_i)$ is the scoring function that evaluates the relevance of the query $Q$ and passage(or document) $P_i$.
$$P^{rank} = \operatorname{TopK}_{i\in P} R(Q,P_i) \quad\quad (k\leq len(P))$$
There three main methods of LTR based on the current literature, Pointwise (give each passage a score), Pairwise (compare two passages each time) and Listwise (compare all the passages at once) [2] [3]. Pointwise faces issues with less relavance analysis between passages. Pairwise’s weakness is huge time complexity even with optimized sorted method, such as heap sort or quick sort ($O(k\cdot \log_{2}{N})$). The downside of Listwise is limited context window of LLMs [3].

The evaluation metric is usually $NDCG@k$, and $rel_i$ means the real relavance score of the i-th item in ranked list. $IDCG@k$ is the maximum possible DCG with ideal ranking. The range of $NDCG@k$ is [0, 1], higher values indicate better ranking quality.
$$NDCG@k = \frac{DCG@k}{IDCG@k} \ DCG@k = \sum_{i=1}^{k} \frac{rel_i}{\log_2(i+1)} \quad IDCG@k = \sum_{i=1}^{k} \frac{rel_{\pi(i)}}{\log_2(i+1)} \
$$
- Setwise [2] enables ranking by evaluating small groups of documents in a singe LLM inference. Instead of comparing each document pair independently (Pairwise) or attempting to rank them at once (Listwise).
- Setwise Insertion [3] extend the Setwise with previous ranking infomation, saving the query time and prompt usage.
Re-ranking
LLM in recommendation scenario are used for reranking the recommender ranking results for better scalability, personalization of the results.
- LLM4Rerank [1] constructs a finite-state machine composed of different function nodes, and a reranking process is a complete iteration of this machine.

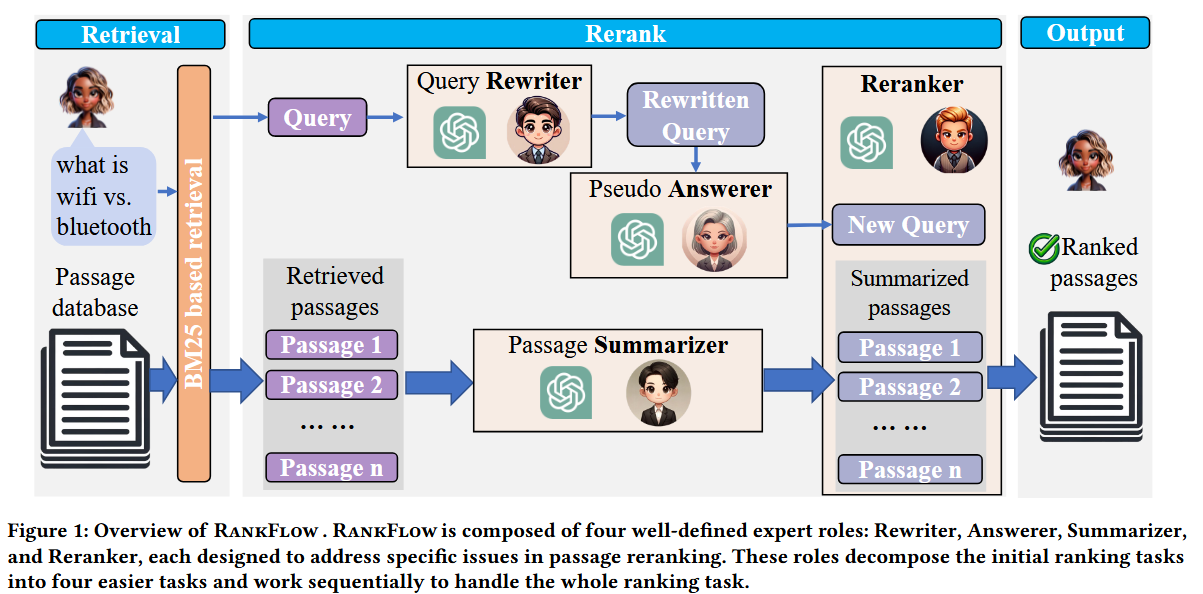
- RankFlow [4] utilizes LLMs to rewrite the query and summarize the passages, and rerank them.
- Movin et al. [5] do a empirical study about the zero-shot reranking with LLM for structed data. The authors find that zero‑shot LLMs like GPT‑4 can act as rerankers on datasets with many precomputed features, but overall they still underperform traditional supervised methods such as LambdaMART. However, on difficult queries where the baseline fails, LLM reranking can surpass it, though results remain brittle and highly sensitive to prompt design.
